Minimum Spanning Tree
A spanning tree of a graph consists of all nodes of the graph and some of the edges of the graph so that there is a path between any two nodes. Like trees in general, spanning trees are connected and acyclic. Usually there are several ways to construct a spanning tree.
Properties of Minimum Spanning Tree :
- A minimum spanning tree of a graph is unique, if the weight of all the edges are distinct. Otherwise, there may be multiple minimum spanning trees. (Specific algorithms typically output one of the possible minimum spanning trees).
- Minimum spanning tree is also the tree with minimum product of weights of edges. (It can be easily proved by replacing the weights of all edges with their logarithms)
- In a minimum spanning tree of a graph, the maximum weight of an edge is the minimum possible from all possible spanning trees of that graph. (This follows from the validity of Kruskal's algorithm).
- The maximum spanning tree (spanning tree with the sum of weights of edges being maximum) of a graph can be obtained similarly to that of the minimum spanning tree, by changing the signs of the weights of all the edges to their opposite and then applying any of the minimum spanning tree algorithm.
A minimum spanning tree is a spanning tree whose weight is as small as possible.
A MST has V-1 edges.
Real Life Application :
- Building road networks for different cities.
Alortihms for finding Minimum Spanning Tree :
- Prism’s Algorithm
- Kruskal’s Algorithm
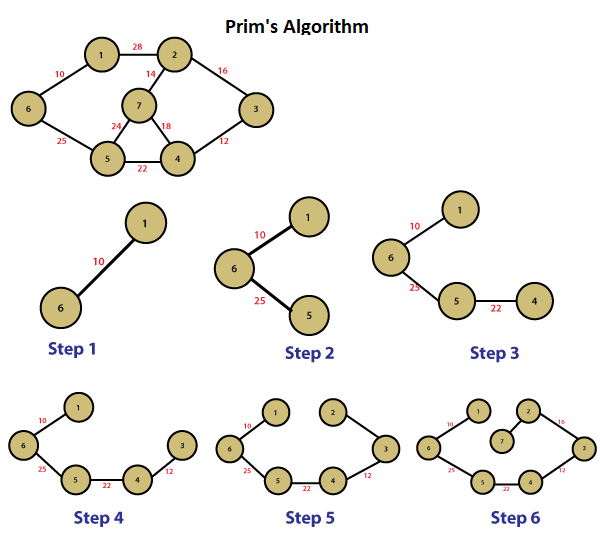
Prim’s Algorithm :
The minimum spanning tree is built gradually by adding edges one at a time. At first the spanning tree consists only of a single vertex (chosen arbitrarily). Then the minimum weight edge outgoing from this vertex is selected and added to the spanning tree. After that the spanning tree already consists of two vertices. Now select and add the edge with the minimum weight that has one end in an already selected vertex (i.e. a vertex that is already part of the spanning tree), and the other end in an unselected vertex. And so on, i.e. every time we select and add the edge with minimal weight that connects one selected vertex with one unselected vertex. The process is repeated until the spanning tree contains all vertices (or equivalently until we have n−1 edges).
class Graph {
int V;
vector<pair<int, int>> *l;
public:
Graph(int n) {
V = n;
l = new vector<pair<int, int>>[n];
}
void addEdge (int x, int y, int w) {
l[x].push_back({y, w});
l[y].push_back({x, w});
}
int prim_mst () {
// Init a Min Heap
// this looks complex but its just opposite of priority_queue<pair<int, int>> Q
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> Q;
// visited array to get weather a node has been visited or not
bool *visited = new bool[V]{0};
int ans = 0;
// begin
Q.push({0, 0}); // weight, node
while (!Q.empty()) {
// pick out the edge with min weight
auto best = Q.top();
Q.pop();
int to = best.second;
int weight = best.first;
if (visited[to]) {
// discard the edge, and continue
continue;
}
// otherwise take the current edge
ans += weight;
visited[to] = 1;
// add the new edges in the queue
for (auto x : l[to]) {
if (visited[x.first] == 0) {
Q.push({x.second, x.first});
}
}
}
}
};
Kruskal’s Algorithm :
Kruskal's algorithm initially places all the nodes of the original graph isolated from each other, to form a forest of single node trees, and then gradually merges these trees, combining at each iteration any two of all the trees with some edge of the original graph. Before the execution of the algorithm, all edges are sorted by weight (in non-decreasing order). Then begins the process of unification: pick all edges from the first to the last (in sorted order), and if the ends of the currently picked edge belong to different subtrees, these subtrees are combined, and the edge is added to the answer. After iterating through all the edges, all the vertices will belong to the same sub-tree, and we will get the answer.
Algorithm :
- Sort edges by their weights.
- Iterate to sorted edges one-by-one.
- Pick an edge add it to our MST if it doesnot form a cycle and belongs to a differrent set.
// dsu finding a cycle
#include <bits/stdc++.h>
using namespace std;
class Graph {
int V;
vector<pair<int, int>> l;
public:
Graph (int n) {
V = n;
}
void addEdge(int x, int y) {
l.push_back({x, y});
}
//Find Function (optimized)
int find (int i, vector<int> &parent) {
if (parent[i] == -1) return i;
else return parent[i] = find (parent[i], parent);
}
//Union Function (optimized)
void unite (int s1, int s2, vector<int> &parent, vector<int> &rank) {
if (rank[s1] > rank[s2]) {
parent[s2] = s1;
rank[s1] += rank[s2];
} else {
parent[s1] = s2;
rank[s2] += rank[s1];
}
}
//contain cycle
bool containCycle () {
vector<int> parent(V, -1);
vector<int> rank(V, 1);
for (auto edge : l) {
int s1 = find (edge.first, parent);
int s2 = find (edge.second, parent);
if (s1 == s2) return true;
else unite(s1, s2, parent, rank);
}
return false;
}
};
int main() {
Graph g(3);
g.addEdge(0, 1);
g.addEdge(0, 2);
cout << g.containCycle(parent);
return 0;
}
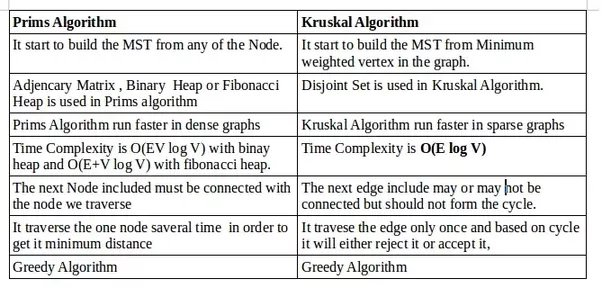
Difference between Prim’s and Kruskal Algorithm :