Graph Traversal
There are two fundamental graph algorithms for traversal : Breadth-First Search and Depth-First Search. Both algorithms are given a starting node in the graph, and they visit all nodes that can be reached from the starting node. The difference in the algorithms is the order in which they visit the nodes.
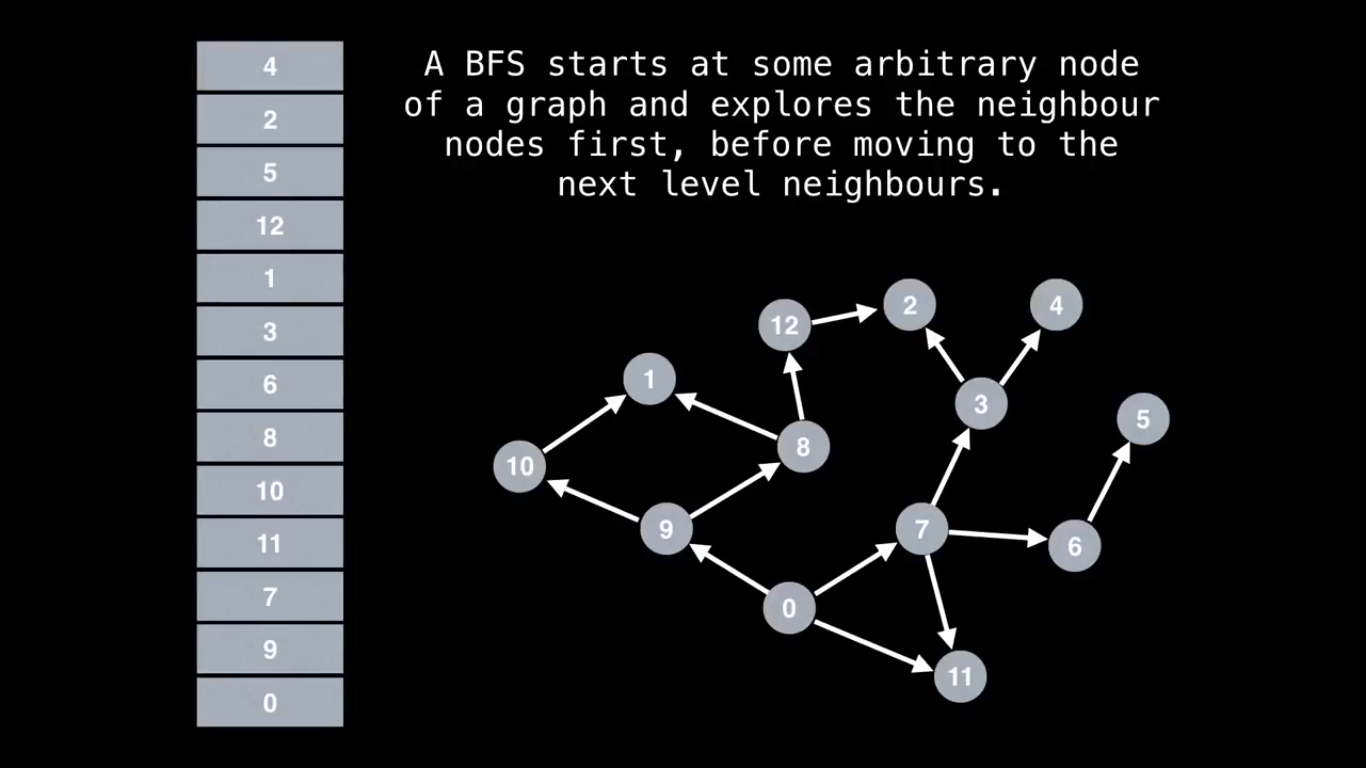
Breadth-First Search (BFS) :
Breadth-first search (BFS) visits the nodes in increasing order of their distance from the starting node. Thus, we can calculate the distance from the starting node to all other nodes using breadth-first search.
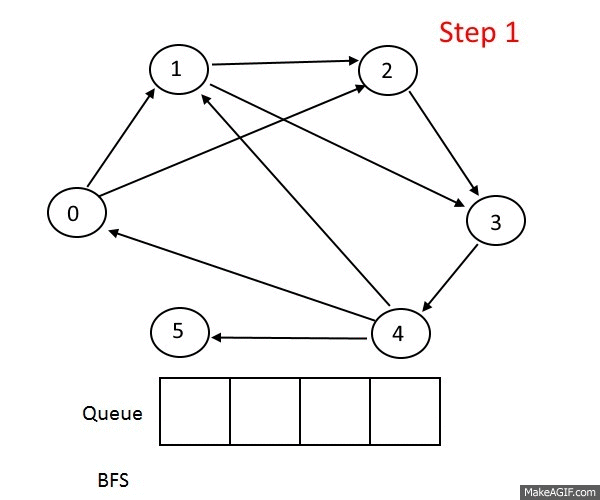
The time complexity of breadth-first search is O(n+ m), where n is the number of nodes and m is the number of edges.
Its implementation is based on a queue that contains nodes. At each step, the next node in the queue will be processed. At each step, the next node in the queue will be processed. The following code assumes that the graph is stored as adjacency lists and maintains the following data structures:
queue<int> q;
bool visited[N];
int distance[N];
The queue q contains nodes to be processed in increasing order of their distance. New nodes are always added to the end of the queue, and the node at the beginning of the queue is the next node to be processed. The array visited indicates which nodes the search has already visited, and the array distance will contain the distances from the starting node to all nodes of the graph.
The search can be implemented as follows, starting at node x:
visited[x] = true;
distance[x] = 0;
q.push(x);
while (!q.empty()) {
int s = q.front(); q.pop();
// process node s
for (auto u : adj[s]) {
if (visited[u]) continue;
visited[u] = true;
distance[u] = distance[s]+1;
q.push(u);
}
}
Breadth-First Search Code:
#include <bits/stdc++.h>
using namespace std;
class Graph {
int V;
list<int> *l;
public:
Graph (int v) {
V = v;
l = new list<int>[V];
}
void addEdge (int i, int j, bool undir=true) {
l[i].push_back(j);
if (undir) l[j].push_back(i);
}
void printAdjList () {
for (int i=0; i<V; i++) {
cout << i << "-->";
for (auto node : l[i]) cout << node << ",";
cout << "\n";
}
}
void bfs(int source) {
queue<int> q;
bool *visited = new bool[V]{0}; // initialized 0
q.push(source);
visited[source] = true;
while(!q.empty()) {
//do some work for every node
int f = q.front();
cout << f << " ";
q.pop();
//push nbr of current node inside queue
for (auto nbr: l[f]) {
if (!visited[nbr]) {
q.push(nbr);
visited[nbr] = true;
}
}
}
}
};
int main () {
Graph g(6);
g.addEdge(0,1);
g.addEdge(0,4);
g.addEdge(2,1);
g.addEdge(3,4);
g.addEdge(4,5);
g.addEdge(2,3);
g.addEdge(3,5);
g.printAdjList();
g.bfs(1);
return 0;
}
//output:
//
// 0-->1,4,
// 1-->0,2,
// 2-->1,3,
// 3-->4,2,5,
// 4-->0,3,5,
// 5-->4,3,
// 1 0 2 4 3 5
Shortest path from source to node in undirected graph
#include <bits/stdc++.h>
using namespace std;
class Graph {
int V;
list<int> *l;
public:
Graph (int v) {
V = v;
l = new list<int>[V];
}
void addEdge (int i, int j, bool undir=true) {
l[i].push_back(j);
if (undir) l[j].push_back(i);
}
void printAdjList () {
for (int i=0; i<V; i++) {
cout << i << "-->";
for (auto node : l[i]) cout << node << ",";
cout << "\n";
}
}
void bfs(int source) {
queue<int> q;
bool *visited = new bool[V]{0};
int *dist = new int[V]{0};
int *parent = new int[V];
for (int i=0; i<V; i++) parent[i] = -1;
q.push(source);
visited[source] = true;
parent[source] = source;
dist[source] = 0;
while(!q.empty()) {
//do some work for every node
int f = q.front();
cout << f;
q.pop();
//push nbr of current node inside queue
for (auto nbr: l[f]) {
if (!visited[nbr]) {
q.push(nbr);
parent[nbr] = f;
dist[nbr] = dist[f]+1;
visited[nbr] = true;
}
}
}
cout << "\n";
//print shortest distance
for (int i=0; i<V; i++) {
cout << "Shortest dist to " << i << " is " << dist[i] << "\n";
}
//print the path from a source to any destination
int dest = 5;
if (dest != -1) {
int temp = dest;
while(temp!=source) {
cout << temp << " -- ";
temp = parent[temp];
}
cout << source << "\n";
}
}
};
int main () {
Graph g(6);
g.addEdge(0,1);
g.addEdge(0,4);
g.addEdge(2,1);
g.addEdge(3,4);
g.addEdge(4,5);
g.addEdge(2,3);
g.addEdge(3,5);
g.printAdjList();
g.bfs(1);
return 0;
}
//output:
//
// 0-->1,4,
// 1-->0,2,
// 2-->1,3,
// 3-->4,2,5,
// 4-->0,3,5,
// 5-->4,3,
// 102435
// from 1
// Shortest dist to 0 is 1
// Shortest dist to 1 is 0
// Shortest dist to 2 is 1
// Shortest dist to 3 is 2
// Shortest dist to 4 is 2
// Shortest dist to 5 is 3
// 5 -- 4 -- 0 -- 1
Depth-First Search :
Depth-first search (DFS) is a straightforward graph traversal technique. The algorithm begins at a starting node, and proceeds to all other nodes that are reachable from the starting node using the edges of the graph.
Depth-first search always follows a single path in the graph as long as it finds new nodes. After this, it returns to previous nodes and begins to explore other parts of the graph. The algorithm keeps track of visited nodes, so that it processes each node only once.
The time complexity of depth-first search is O(n+ m) where n is the number of nodes and m is the number of edges, because the algorithm processes each node and edge once.
Depth-first search can be conveniently implemented using recursion. The following function dfs begins a depth-first search at a given node. The function assumes that the graph is stored as adjacency lists in an array.
vector<int> adj[N];
and also maintains an array
bool visited[N];
that keeps track of the visited nodes. Initially, each array value is false, and when the search arrives at node s, the value of visited[s] becomes true. The function can be implemented as follows:
void dfs(int s) {
if (visited[s]) return;
visited[s] = true;
// process node s
for (auto u: adj[s]) {
dfs(u);
}
}
Depth-First Search Code :
#include <bits/stdc++.h>
using namespace std;
class Graph {
int V;
list<int> *l;
public:
Graph(int v) {
V = v;
l = new list<int>[V];
}
void addEdge(int i, int j, bool undir = true) {
l[i].push_back(j);
if (undir) l[j].push_back(i);
}
void printAdjList() {
for (int i = 0; i < V; i++) {
cout << i << "-->";
for (auto node : l[i]) cout << node << ",";
cout << "\n";
}
}
void dfsHelper(int node, bool *visited) {
visited[node] = true;
cout << node << " ";
// make a dfs call on all its unvisited neighbours
for (int nbr : l[node]) {
if (!visited[nbr]) dfsHelper(nbr, visited);
}
return;
}
void dfs(int source) {
bool *visited = new bool[V]{0};
dfsHelper(source, visited);
}
};
int main() {
Graph g(6);
g.addEdge(0, 1);
g.addEdge(0, 4);
g.addEdge(2, 1);
g.addEdge(3, 4);
g.addEdge(4, 5);
g.addEdge(2, 3);
g.addEdge(3, 5);
g.printAdjList();
g.dfs(1);
return 0;
}
// output
// 0-->1,4,
// 1-->0,2,
// 2-->1,3,
// 3-->4,2,5,
// 4-->0,3,5,
// 5-->4,3,
// 1 0 4 3 2 5