Graph Introduction and Representation

What is a Graph ? 🤔

A Graph is a non-linear data structure consisting of nodes (or vertices) and edges. Edges are the lines that connect two nodes in the graph.

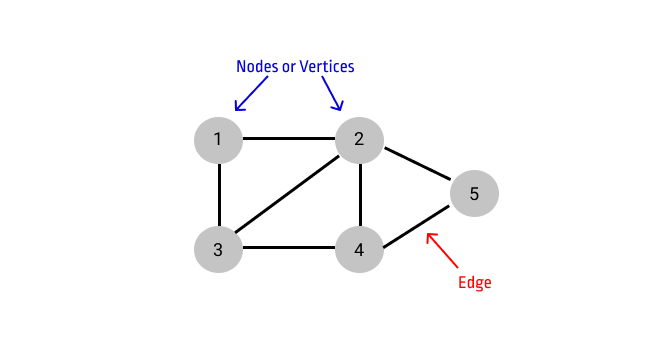
Types of Graphs :

Some of the useful types of graphs are :

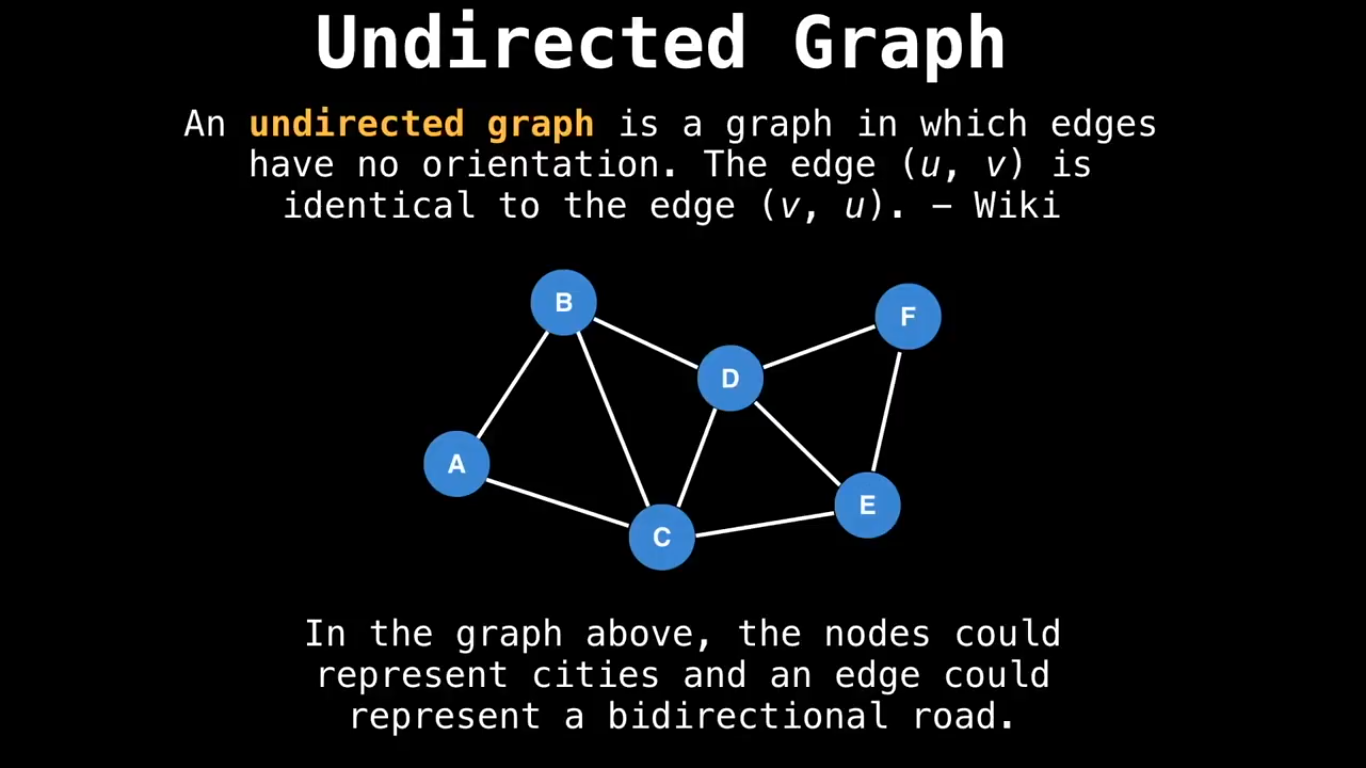
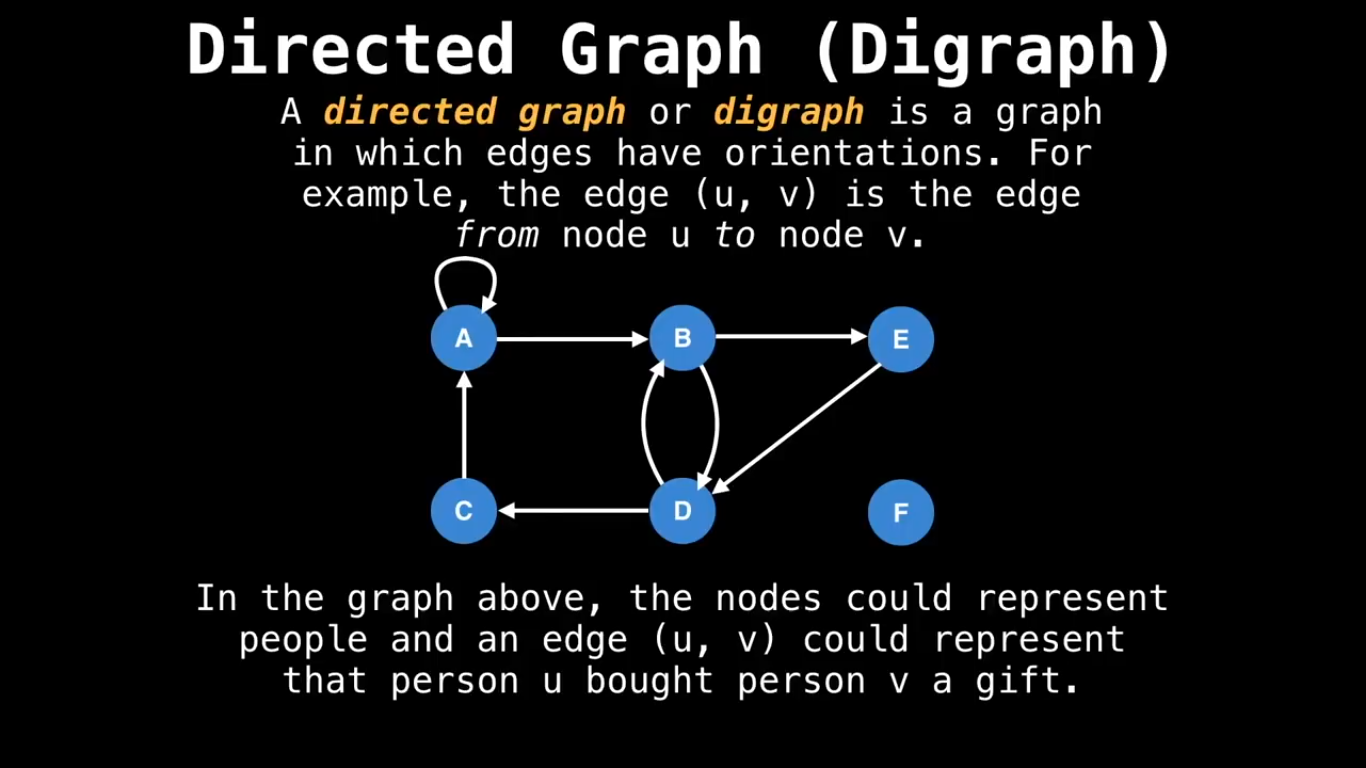
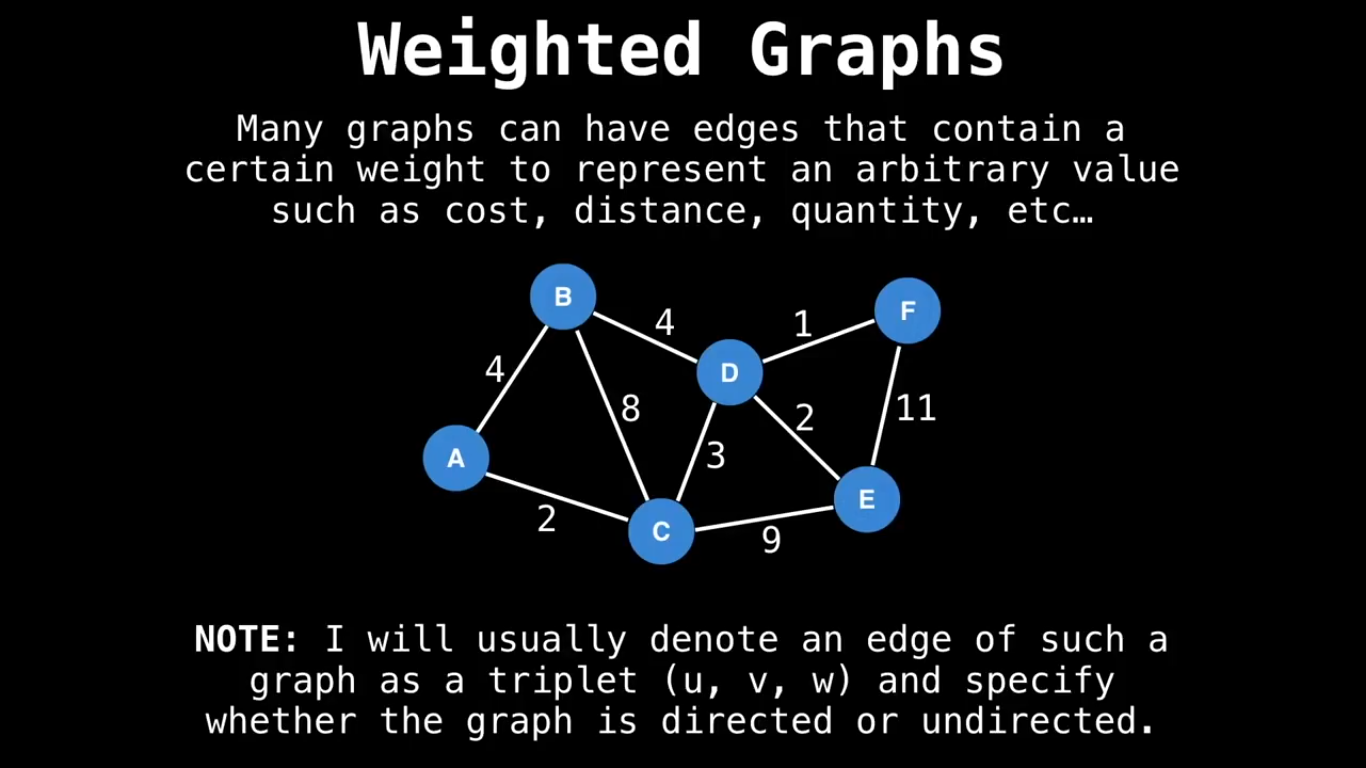
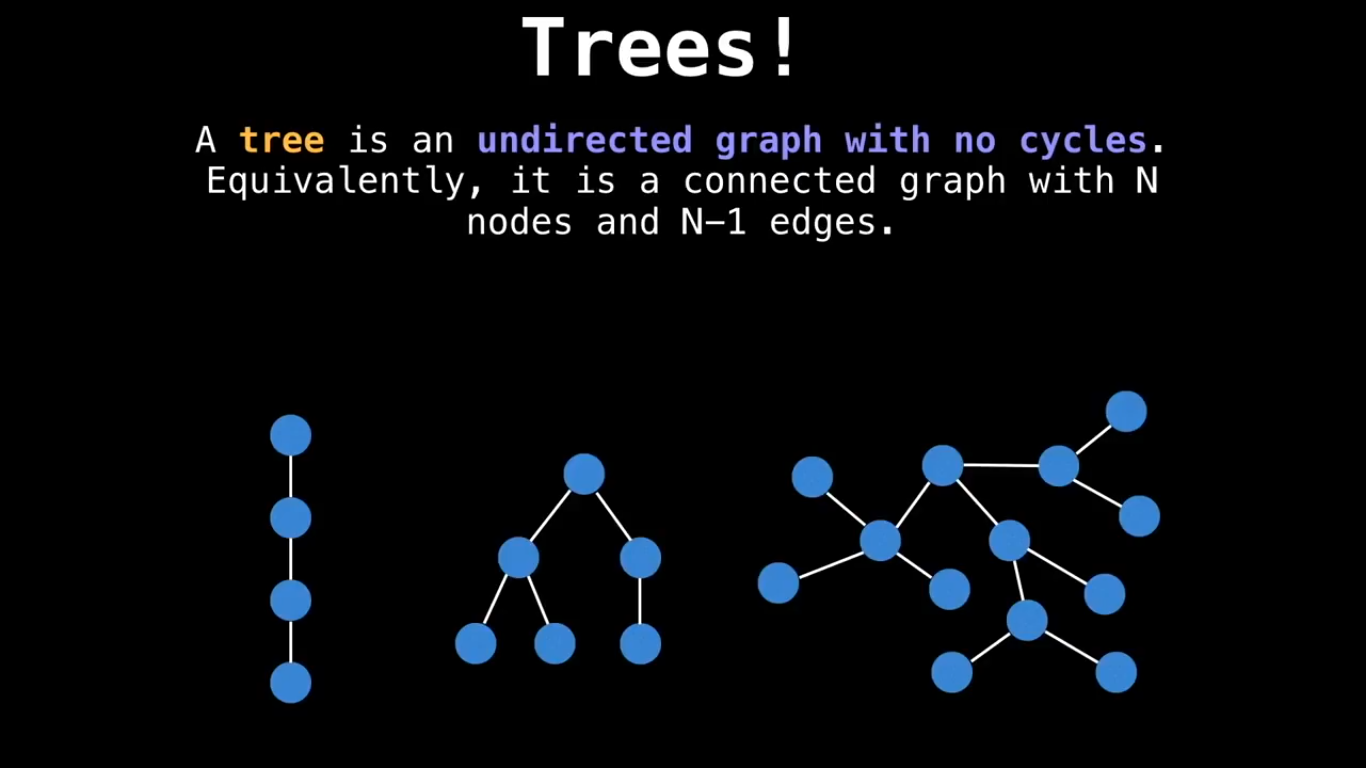
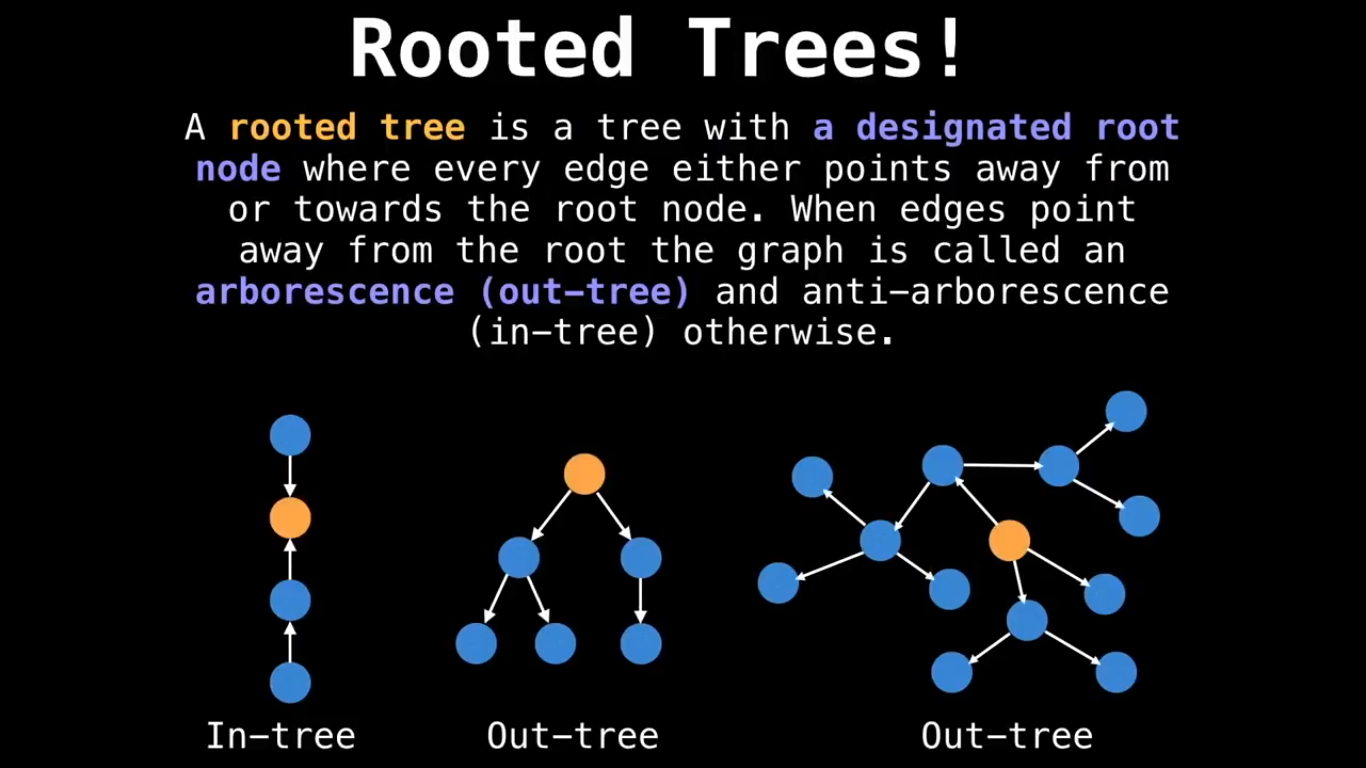
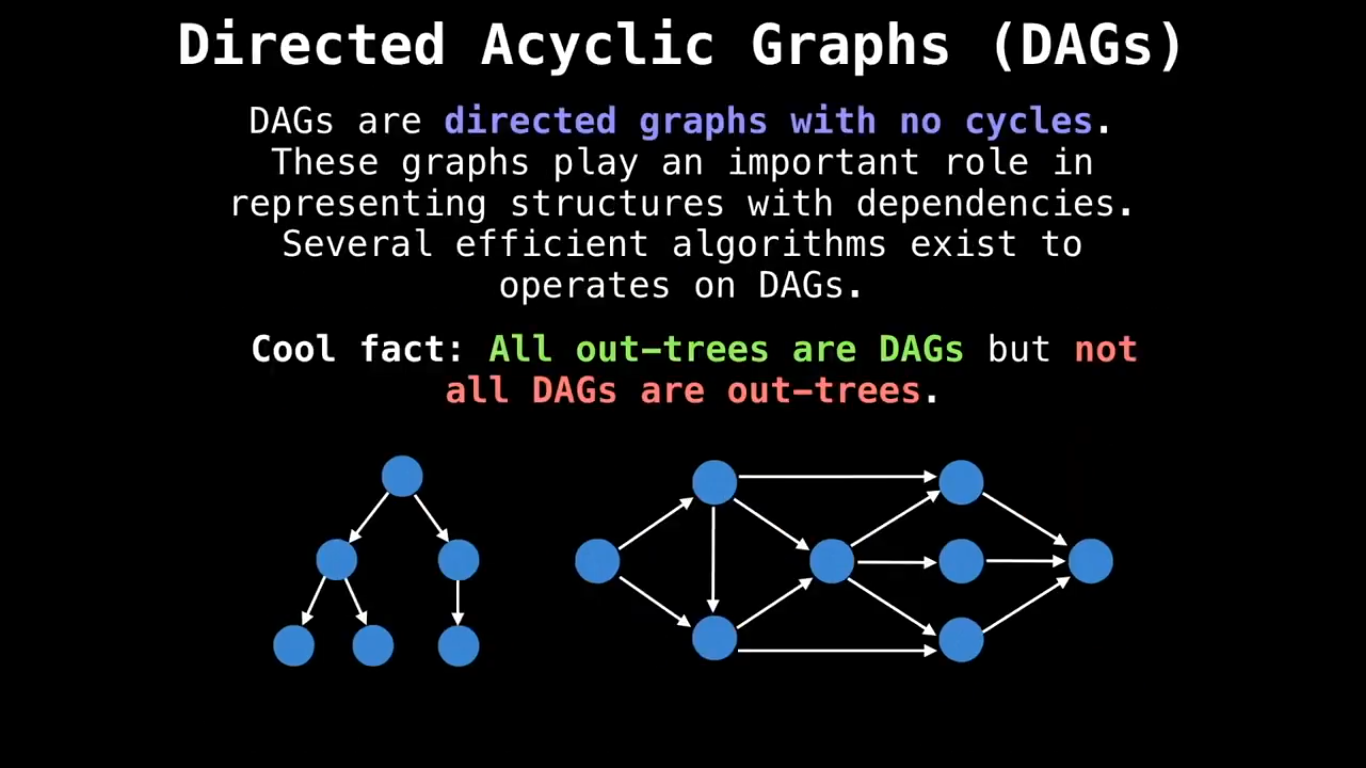
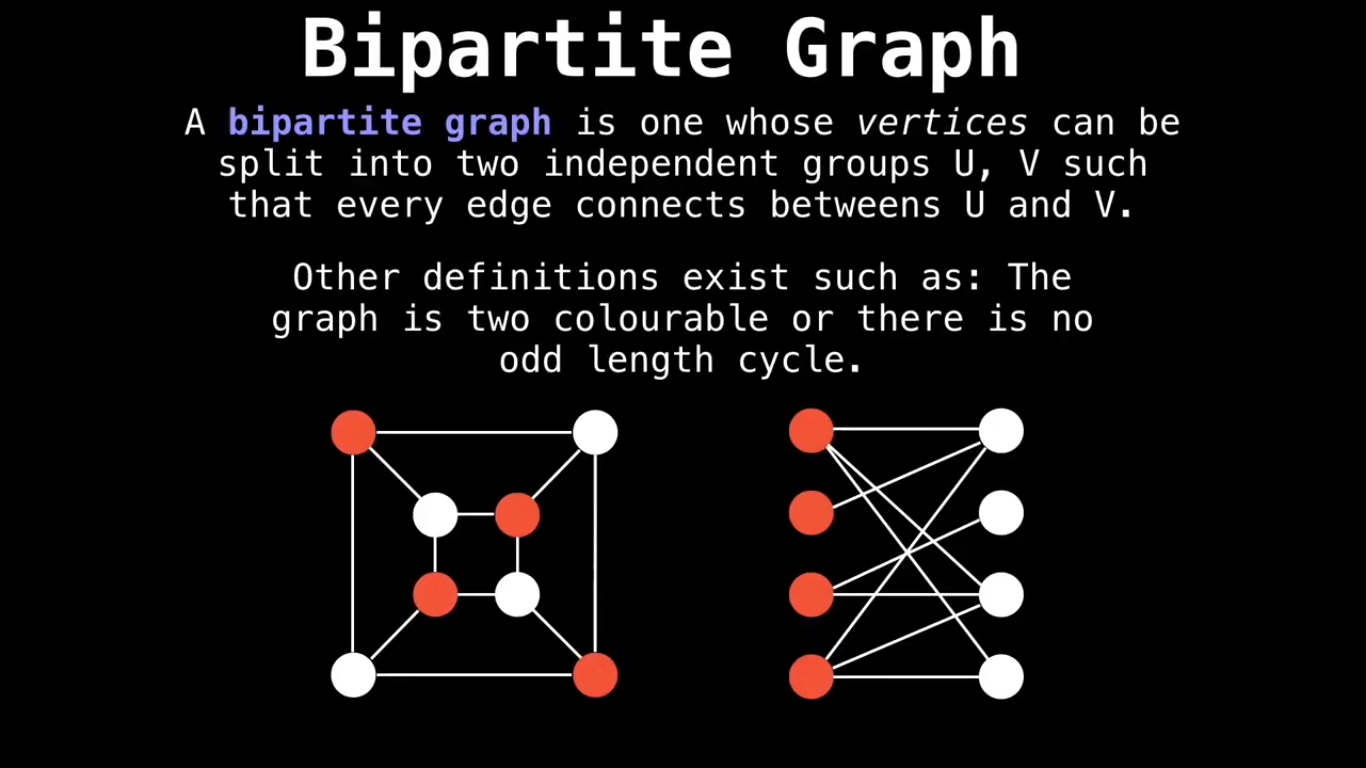
Some special types of Graph :

Representation of Graphs :

Methods of representing or storing of graphs are :

• Adjacency List
• Adjacency Matrix
• Edge List
• 2D Matrix (Implicit Graph)

Adjacency List Representation :

In the adjacency list representation, each node x in the graph is assigned an adjacency list that consists of nodes to which there is an edge from x. Adjacency lists are the most popular way to represent graphs, and most algorithms can be efficiently implemented using them.

A convenient way to store the adjacency lists is to declare an array of vectors as follows:

vector<int> adj[N];

If the graph is undirected, it can be stored in a similar way, but each edge is added in both directions. For a weighted graph, the structure can be extended as follows:

vector<pair<int,int>> adj[N];

In this case, the adjacency list of node a contains the pair (b,w) always when there is an edge from node a to node b with weight w.

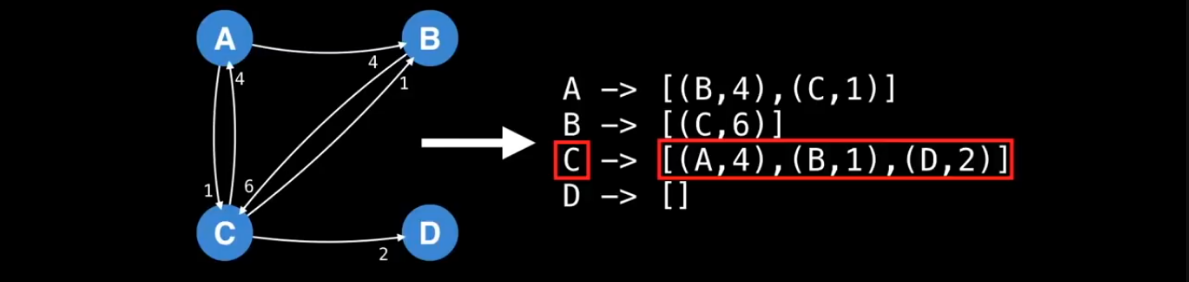
Adjecency List Representation using C++ :

#include <bits/stdc++.h>
using namespace std;

class Graph {
  int V;
  list<int> *l;
	
  public:
    Graph (int v) {
      V = v;
      l = new list<int>[V];  // here list is used insted of vector.
      // array, list , vector, hashmap anything can be used
    }
		
    void addEdge (int i, int j, bool undir=true) {
      l[i].push_back(j);
      if (undir) l[j].push_back(i);
    }
		
    void printAdjList () {
      for (int i=0; i<V; i++) {
        cout << i << "-->";
        for (auto node : l[i]) cout << node << ",";
        cout << "\n";
      }
		}
};

int main () {
  Graph g(6);
  g.addEdge(0,1);
  g.addEdge(0,4);
  g.addEdge(2,1);
  g.addEdge(3,4);
  g.addEdge(4,5);
  g.addEdge(2,3);
  g.addEdge(3,5);
  g.printAdjList();
	
  return 0;
}

//output:

0-->1,4,
1-->0,2,
2-->1,3,
3-->4,2,5,
4-->0,3,5,
5-->4,3,

Another Method :

#include <bits/stdc++.h>
using namespace std;

class Node {
  public:
    string name;
    list<string> neighbours;
		
    Node(string name) {
      this->name = name;
    }
};

class Graph {
  //All Nodes
  //Hashmap (string, Node*)
	
  unordered_map<string, Node*> m;
	
  public:
    Graph(vector<string> cities) {
      for(auto city: cities) {
        m[city] = new Node(city);
      }
    }
		
    void addEdge(string x, string y, bool undir=true) {
      m[x]->neighbours.push_back(y);	
			
      if (undir) m[y]->neighbours.push_back(x);
    }
		
    void printAdjList() {
      for (auto cityPair : m) {
        auto city = cityPair.first;
        Node  *node = cityPair.second;
        cout << city << "-->";
        for (auto nbr : node->neighbours) {
          cout << nbr << ",";
        }
        cout << "\n";
      }
    }
};

int main () {
  vector<string> cities = {"Delhi", "London", "Paris", "New York"};
  Graph g(cities);
	
  g.addEdge("Delhi", "London");
  g.addEdge("New York", "London");
  g.addEdge("Delhi", "Paris");
  g.addEdge("Paris", "New York");
  g.printAdjList();
	
  return 0;
}

//output:

New York-->London,Paris,
Paris-->Delhi,New York,
Delhi-->London,Paris,
London-->Delhi,New York,

Adjacency Matrix Representation :

An adjacency matrix is a two-dimensional array that indicates which edges the graph contains. We can efficiently check from an adjacency matrix if there is an edge between two nodes. The matrix can be stored as an array :

int adj[N][N];

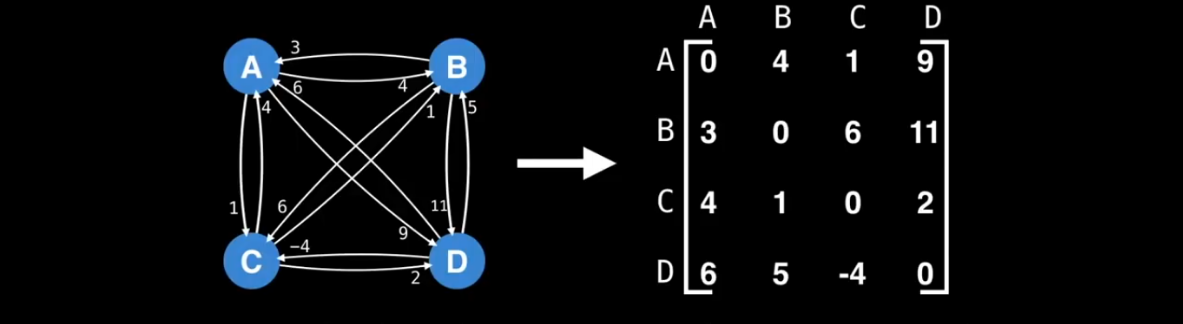
If the graph is weighted, the adjacency matrix representation can be extended so that the matrix contains the weight of the edge if the edge exists.

Edge List Representation :

An edge list contains all edges of a graph in some order. This is a convenient way to represent a graph if the algorithm processes all edges of the graph and it is not needed to find edges that start at a given node. The edge list can be stored in a vector :

vector<pair<int,int>> edges;

where each pair (a,b) denotes that there is an edge from node a to node b.

If the graph is weighted, the structure can be extended as follows:

vector<tuple<int,int,int>> edges;

Each element in this list is of the form (a,b,w), which means that there is an edge from node a to node b with weight w.

Implicit Graph :

Explicit Graph:

• All vertices are identified individually and represented separatedly.
• All edges are identified individually and represented separatedly.

Implicit Graph:

• Only a subset, possibly only one, of the vertices is given an explicit representation. (The others are implied.)
• Only a subset, and possibly zero, of the edges is given an explicit representation.
• A set of “operators” is provided that can be used to construct “new” edges and vertices.

Example of Implicit Graph:

Collatz conjecture -

• If the number is even, divide it by two.
• If the number is odd, triple it and add one.

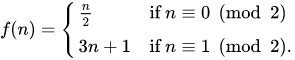
This process will eventually reach the number 1, regardless of which positive integer is chosen initially.

Image Sources - Google Images, William Fiset youtube video