Cycle Detection in Graphs

Every graph without a cycle is a Tree. If a graph contains a cycle then we have a way to visit node more than one time.

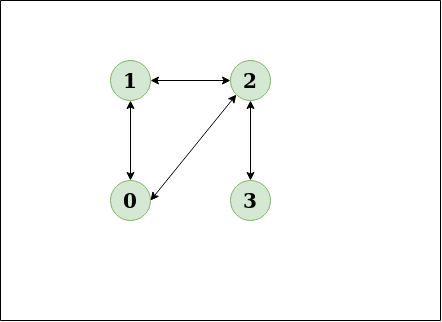
Cycle Detection in Undirected Graphs :

An Undirected Graph contains a cycle if next node is already visited and next node is not parent node of current node.

Using Depth-First Search (DFS) :

#include <bits/stdc++.h>
using namespace std;

class Graph {
  int V;
  list<int> *l;

 public:
  Graph(int v) {
    V = v;
    l = new list<int>[V];
  }

  void addEdge(int i, int j, bool undir = true) {
    l[i].push_back(j);
    if (undir) l[j].push_back(i);
  }

  bool dfs(int node, vector<bool> &visited, int parent) {
    // mark that node visited
    visited[node] = true;
    for (auto nbr : l[node]) {
      if (!visited[nbr]) {
        bool foundACycle = dfs(nbr, visited, node);
        if (foundACycle) return true;
      } else if (nbr != parent)
        return true;
    }
    return false;
  }

  bool contains_cycle() {
    // graph is a single component
    vector<bool> visited(V, false);
    return dfs(0, visited, -1);
  }
};

int main() {
  Graph g(6);
  g.addEdge(0, 1);
  g.addEdge(0, 4);
  g.addEdge(2, 1);
  g.addEdge(3, 4);
  g.addEdge(4, 5);
  g.addEdge(2, 3);
  g.addEdge(3, 5);
  cout << g.contains_cycle();  // 1
  return 0;
}

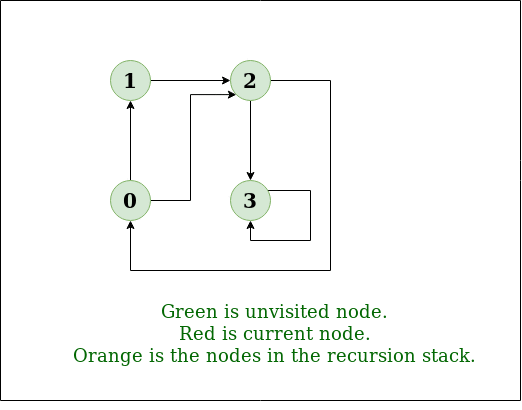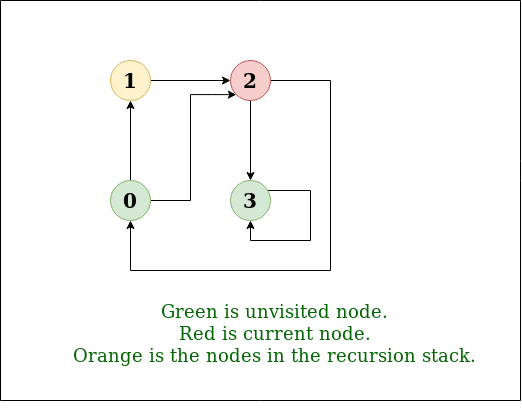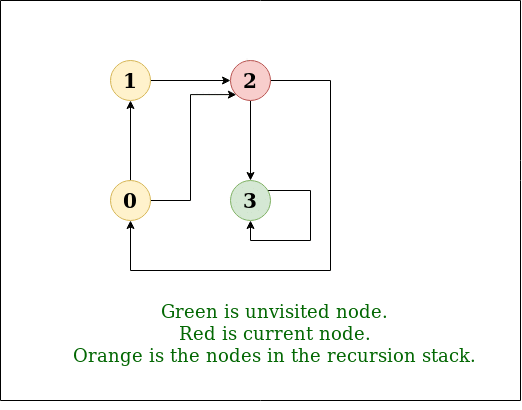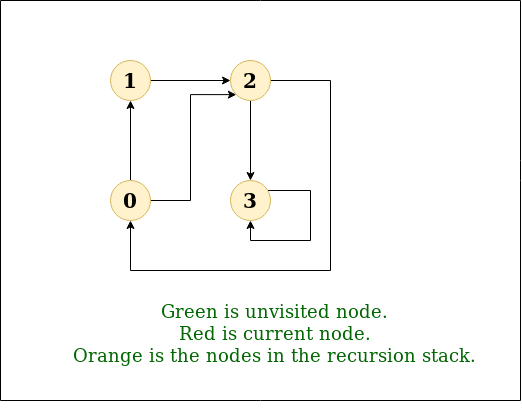
Cycle Detection in Directed Graph :

In Directed Graph we store both visited nodes and nodes of current path (using stack). If next node is visited and also in current path then the graph contains a cycle.

#include <bits/stdc++.h>
using namespace std;

class Graph {
  int V;
  list<int> *l;

 public:
  Graph(int v) {
    V = v;
    l = new list<int>[V];
  }

  void addEdge(int i, int j, bool undir = false) {
    l[i].push_back(j);
    if (undir) l[j].push_back(i);
  }

  bool dfs(int node, vector<bool> &visited, vector<bool> &stack) {
    // return true if backedge is found, else return false
    // arrive at node
    visited[node] = true;
    stack[node] = true;

    for (int nbr : l[node]) {
      if (stack[nbr])
        return true;
      else if (!visited[nbr]) {
        bool nbrFoundACycle = dfs(nbr, visited, stack);
        if (nbrFoundACycle) return true;
      }
    }

    // going back
    stack[node] = false;
    return false;
  }

  bool contains_cycle() {
    vector<bool> visited(V, false);
    vector<bool> stack(V, false);

    for (int i = 0; i < V; i++) {
      int source = i;
      if (!visited[source]) {
        if (dfs(source, visited, stack)) return true;
      }
    }
    return false;
  }
};

int main() {
  Graph g1(3);
  g1.addEdge(0, 1);
  g1.addEdge(1, 2);
  g1.addEdge(2, 0);
  cout << g1.contains_cycle() << "\n";  //1

  Graph g2(3);
  g2.addEdge(0, 1);
  g2.addEdge(1, 2);
  cout << g2.contains_cycle() << "\n";  //0

  return 0;
}

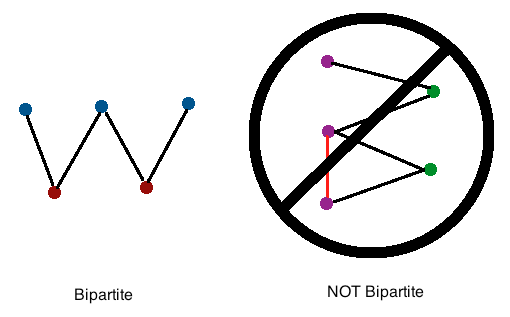
Bipartite Graph :

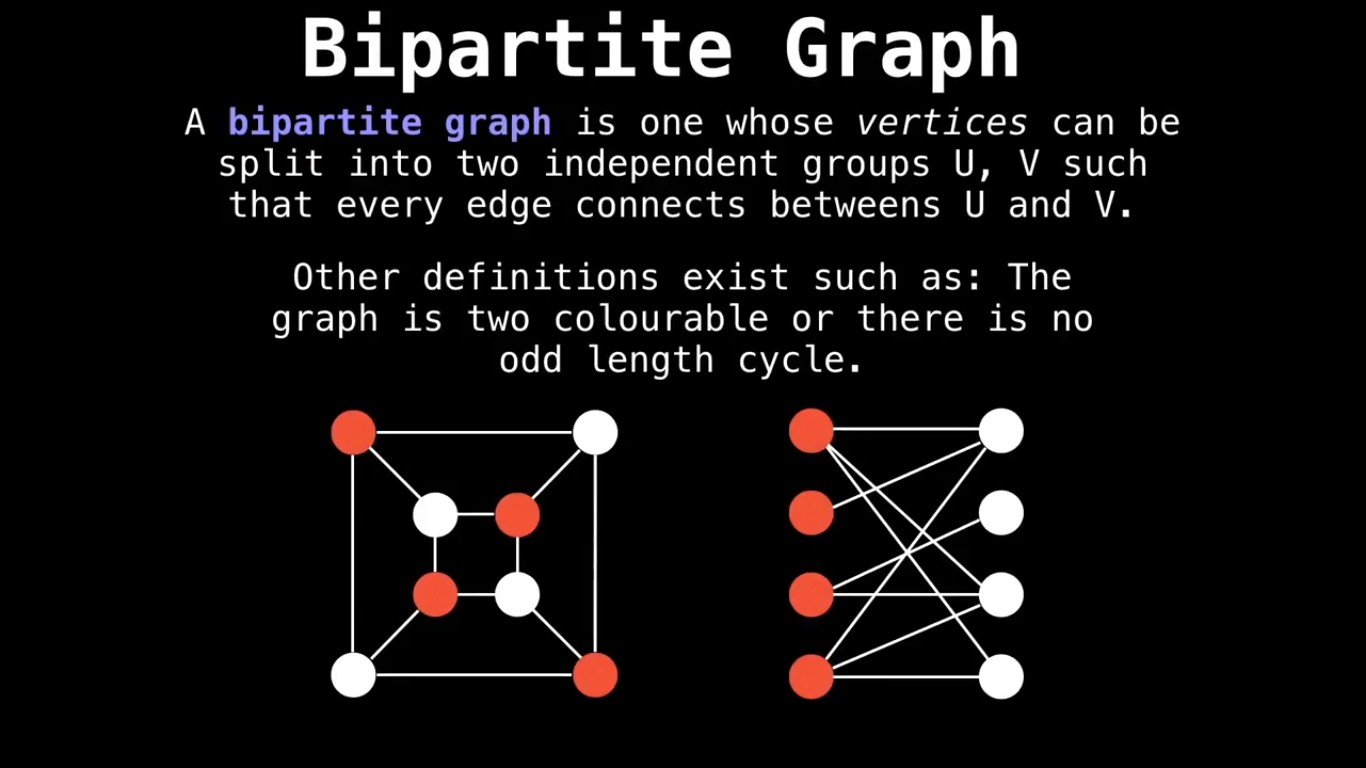
Bipartite graphs may be characterized in several different ways:

• A graph is bipartite if and only if it does not contain an odd cycle.
• A graph is bipartite if and only if it is 2-colorable, (i.e. its chromatic number is less than or equal to 2).
• Any bipartite graph consisting of n vertices can have at most n^{2}/4 edges.
• The spectrum of a graph is symmetric if and only if it is a bipartite graph.

#include <bits/stdc++.h>
using namespace std;

class Graph {
  int V;
  list<int> *l;

 public:
  Graph(int v) {
    V = v;
    l = new list<int>[V];
  }

  void addEdge(int i, int j, bool undir = true) {
    l[i].push_back(j);
    if (undir) l[j].push_back(i);
  }

  bool dfsHelper(int node, int *visited, int parent, int color) {
    visited[node] = color;

    for (auto nbr : l[node]) {
      if (visited[nbr] == 0) {
        int subProblem = dfsHelper(nbr, visited, node, 3 - color);
        if (!subProblem) return false;
      } else if (nbr != parent and color == visited[nbr]) {
        return false;
      }
    }
    return true;
  }

  bool isBipartite() {
    int visited[V] = {0};
    int color = 1;
    return dfsHelper(0, visited, -1, color);
  }
};

int main() {
  // by coloring nodes at each step
  // if current node has color 1
  // then adjacent on should have color 2
  Graph g1(3);
  g1.addEdge(0, 1);
  g1.addEdge(1, 2);
  g1.addEdge(2, 0);
  cout << g1.isBipartite() << "\n";  //0

  Graph g2(4);
  g2.addEdge(0, 1);
  g2.addEdge(1, 2);
  g2.addEdge(2, 3);
  g2.addEdge(3, 0);
  cout << g2.isBipartite() << "\n";  //1

  return 0;
}